[28]従動力を受ける薄肉殻の大変形に伴う抵抗機構（英文）

Thomas George、岡田博雄（大阪府大）、福地信義（九大）

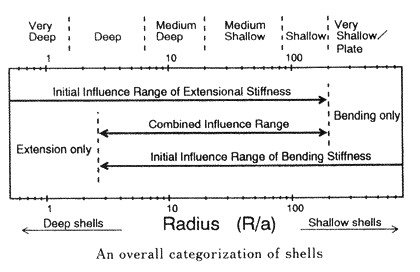
薄肉シェルは曲率の小さいものから大きいものまでそれぞれ外力に対して抵抗するメカニズムが様々である。本論文では一般埋め込み座標系を用いて従動力が作用する場合の支配方程式の伸びと曲げの剛性が支配する領域を厳密に解析する。さらに、面内変位、クリストッフェル記号、混合変量の曲率テンソルなどの役割を明らかにし、部分球殻と円筒殻の場合に初期段階から大変形までの抵抗機構を整理することによって曲率を分類した。

[29] Discrete Optimization of Ship Structures with Genetic Algorithms

信川寿、周国強（広大）

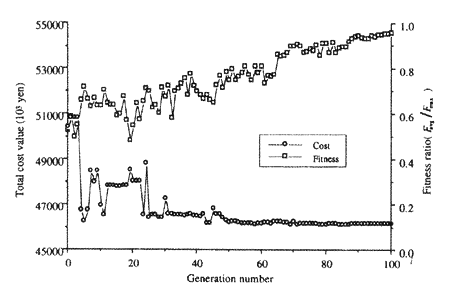
We develop a discrete optimization method for ship structures with genetic algorithms. The constrained cost minimization problem is transformed into an uncostrained maximization of fitness function. Numerical analyses show that the genetic algorithm can handle the discrete optimization problems well only if the discrete design variables are coded into a binary string. Although the genetic algorithm is slower compared to the multiplier method, it may search a better solution as a population processing method.

[30]二次元弾塑性有限要素解析における事後誤差評価に基づいた順応型要素分割

北村充、信川寿（広大）、施建剛（広大大学院）、大坪英臣（東大）

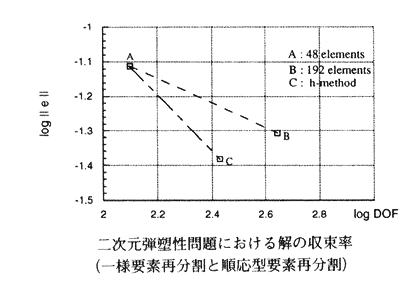
有限な自由度を用いて近似解を求める有限要素解析の精度はメッシュの良し悪しに大きく依存する。各要素の事後誤差ノルムが一様になったとき、全解析領域の事後誤差ノルムは最小になる。この性質を利用して、本報告は有限要素解の事後誤差ノルム分布に従った順応型要素再分割法を検討した。二次元弾塑性問題を対象とした順応型要素再分割法（r型、h型）により有限要素解の大幅な精度向上が確認された。

[31]ソースを用いた新しい有限要素の開発

（第2報：板曲げ要素）

根本勲、多田剛（IHI）

前報で、著者らはソースを用いた新しい有限要素の基礎原理と本手法の有効性を、静弾性問題における2次元平面応力要素および3次元ソリッド要素への適用例で示した。

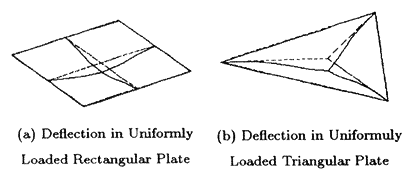
今回、筆者らは薄板の曲げ問題に対する新しいFESを開発した。本要素を用いれば、前報と同様、少ない節点数および要素数で既存の有限要素をはるかにしのぐ非常に良好な計算精度が得られる。特に板曲げ問題では支配方程式の微分の階数が大きいため、半解析的な手法である本手法は、内挿関数を使用する既存のFEMよりも有利である。

前ページ　　　目次へ　　　次ページ